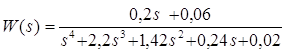| Главная » Статьи » Информатика | [ Добавить статью ] |
|
В противоположность частотным методам, которые оперируют частотными характеристиками, существуют методы, оперирующие функциями времени. Все воздействия, вообще говоря, являются функциями времени. Среди них в классической теории управления особую роль играют так называемые типовые воздействия. Строго говоря, и в частотных методах некоторые воздействия играют особую роль. Мы имеем в виду в первую очередь так называемые гармонические воздействия. Все частотные характеристики системы, так или иначе, описывают ее реакцию на гармонические воздействия различной частоты. Во временных методах также существует небольшое число типовых воздействий, реакция на которые представляет первоочередной интерес. Почти все они базируются на единичном ступенчатом воздействии, которое описывается единичной ступенчатой функцией.
1 Типовые воздействия Единичная ступенчатая функция 1(t). С описательной точки зрения это функция, которая равна нулю в отрицательные моменты времени и единице - в положительные. Принципиальным недостатком таких функций является то, что они не дифференцируемы, тогда как основной математической моделью теории автоматического управления является дифференциальное уравнение. Простейшим математическим описанием этой функции времени является следующее:
Она рассматривается как предел непрерывных и дифференцируемых функций времени
Функция
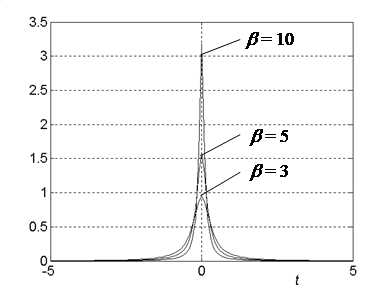
Рисунок 1 - Единичная ступенчатая функцияДельта - функция (d-функция или функция Дирака) определяется как производная от единичной ступенчатой функции. Другими словами,
где в качестве функции В частности, одним из определений d-функция является следующее:
Последовательности функций, сходящиеся к единичной ступенчатой функции и к d-функции при одинаковых значениях параметра b, показаны на рисунках 1 и 2 соответственно. Не смотря на приведенное определение, d-функции нередко рассматривается просто как производная единичной ступенчатой функции Простейшее определение d-функции как функции, равной бесконечности в начале координат и нулю при остальных значениях аргумента мало продуктивно. Широко используются свойства d-функции, которые следуют из его определения как предела последовательности непрерывных функций.
Во-первых, интеграл от d-функции по любой конечной области, включающей начало координат, равен единице. В частности
Это почти очевидно: d-функция является пределом производных последовательности функций, каждая из которых стремится к единице. Другое не менее важное свойство выражается равенством
которое тоже почти очевидно для непрерывных функций, если вспомнить предыдущее свойство. Наряду с этими двумя типовыми воздействиями иногда применяются тесно связанные с ними воздействия: единичная скорость Не трудно доказать, что преобразования Лапласа для этих воздействий:
2 Импульсная переходная функция Передаточная функция
которая называется импульсной переходной характеристикой этой системы. Таким образом, импульсная переходная функция системы – это обратное преобразование от ее передаточной функции. Она столь же полно характеризует систему, что и передаточная функция, так как эти две функции связаны между собой как оригинал и изображение. Импульсная переходная характеристика может быть определена не только как обратное преобразование Лапласа, но и как обратное преобразование Фурье, поскольку оно связано с ним тем же соотношением – прямым и обратным преобразованием Фурье
Фактически, импульсная переходная функция почти никогда не вычисляется в соответствии с этими определениями. Для этой цели используются замечательные свойства самой импульсной переходной функцией и ее связью с другими временными характеристиками системы. Напомним, что преобразование Лапласа выходного процесса равно передаточной функции, умноженной на преобразование Лапласа входного процесса:
и что изображение d - функции равно единице. Подставим в последнее выражение единичное значение изображения входного процесса и убедимся, что импульсная переходная функция равна реакции системы при действии на ее входе d -импульса. Под d - импульсом, как нетрудно догадаться, понимается импульс, математической моделью которого является d - функция. Это объясняет происхождение названия рассматриваемой временной характеристики. Импульсная переходная функция обладает рядом замечательных свойств. Одно из них касается условия устойчивости, а другое – условия физической осуществимости. Импульсная переходная функция
Импульсная переходная функция
Действительно, в любой физически осуществимой системе реакция системы не может наступить раньше причины, ее вызвавшей. В рассматриваемом случае входным воздействием, реакцией на которое является импульсная переходная функция, служит d - импульс, который равен нулю при отрицательных значениях аргумента. Следовательно, и реакция на такое воздействие должна быть равна нулю при отрицательных значениях аргумента. Фактическое определение импульсной переходной функции, как реакции на d - воздействие, связано с определенными трудностями. Во-первых, d - импульс бесконечно большой амплитуды, бесконечно малой длительности и единичной площади можно реализовать только приближенно. При этом суждение о том, достаточно ли малая длительность и достаточно ли большая амплитуда, чтобы реакция системы была достаточно близкой к импульсной переходной функции, сказать трудно. Кроме того, не всякая система допускает подачу на ее вход импульса выше определенной величины. Все сказанное о подобном способе определения имеет отношение только к экспериментам над математическими моделями, но не над физическими объектами. Следующая временная характеристика, с одной стороны, имеет очень простую связь с только что рассмотренной, а с другой стороны, допускает сравнительно простую реализацию. 3 Единичная переходная функция Под единичной переходной функцией понимают реакцию системы на единичное ступенчатое воздействие. Так как изображение по Лапласу единичной ступенчатой функции известно, то не трудно определить изображение по Лапласу
при нулевых начальных условиях. Ясно, что оригинал может быть получен с помощью обратного преобразования найденного изображения. Однако проще воспользоваться каким либо другим способом определения реакции системы на столь простое воздействие. Предложенная интерпретация единичной переходной функции как реакции на единичное ступенчатое воздействие может служить и основой экспериментального определения этой характеристики. Единичное ступенчатое воздействие, как и дельта -функция, является математической идеализацией реальных сигналов, которые предельно резко меняют свое значение с одного уровня на другое. Единственное различие между идеализированном сигналом и реальным – это время перехода из одного состояния в другое. Имея представление о быстродействии исследуемой системы всегда можно сказать, пренебрежимо мало оно или нет. Между единичной переходной характеристикой и импульсной переходной функцией существует очень простая связь. Достаточно определить одну из них как определение другой уже не представляет труда. Не трудно показать, что
Таким образом, импульсная переходная и единичная переходная функции связаны межу собой как производная и интеграл. Другими словами, наряду с только что приведенным выражением справедливо и выражение
4 Связь между входным и выходным процессами во временной области Изображение выходного процесса
Согласно одной из теорем о преобразовании Лапласа, произведению изображений соответствует свертка оригиналов, т.е. из последнего выражения следует
и
В этих выражениях нередко верхний предел интегрирования полагается равным бесконечности. При определенных условиях это можно делать. Для физически осуществимых систем значение импульсной переходной функции равно нулю при отрицательных значениях аргумента, т.е. для таких систем
Поэтому верхний предел в выражении (1) можно устремить к бесконечность, т.е. положить
Именно в такой форме обычно используется выражение выходного процесса через входной во временной (в действительной) области. Нередко в качестве входного воздействия принимается не просто воздействие при нулевых начальных условиях, а равное нулю при отрицательном времени. Однако, если
В приведенных выше выражениях нет уточнения, что считать входным, а что выходным процессом. Эти понятия определяют вместе с определением передаточной функции. Если под входным процессом понимать управляющее воздействие, а в качестве выхода рассматривать сигнал ошибки, то для получения изображения сигнала ошибки следует воспользоваться передаточной функцией по ошибке. Обратное преобразование Лапласа от такой передаточной функции называется импульсной переходной функцией по ошибке. Она позволяет определить сигнал ошибки по выражению входного сигнала (во временной области):
Здесь И вообще, если рассматривать выражения выходного сигнала через внешние воздействия в частотной области как сумму произведений изображений, то в действительной области каждому такому произведению будет соответствовать свертка. Другими словами, выходной процесс системы, на которую действуют управляющее
5 Графические представления частотных характеристик Как уже отмечалось, частотные представления являются основой классических методов теории автоматического управления. С частотных характеристик и началось знакомство с теорией управления. Ведение и использование передаточных функций не означает отклонения от частотного направления. Различие между введенными ранее понятиями частотной характеристики и передаточной функции чисто формальное. Как только заходит речь о графическом представлении, неважно, частотных характеристик или передаточных функций, переменная s в выражении передаточной функции заменяется на переменную jw и изображению подлежит только частотная характеристика. Среди всех графических представлений частотных характеристик особой популярностью пользуются годографы Найквиста и диаграммы Боде. В настоящее время более употребительны диаграммы Боде, но они являются производными от годографов Найквиста, поэтому рассмотрим сначала годографы Найквиста. 1 Годограф Найквиста. Представление частотной характеристики
на плоскости комплексной переменной в зависимости от частоты называется амплитудно-фазовой частотной характеристикой (а.ф.ч.х.). Вообще говоря, с изменением частоты w от нуля до бесконечности (0 < w <¥) вектор На рисунке 1 приведен типичный пример годографа Найквиста в положительном диапазоне частот (0 < w <¥). На нем показаны все составляющие частотной характеристики как комплексной функции вещественного аргумента. Иногда, (например, в ППП Control System Toolbox) годограф строится во всем диапазоне частот (-¥ < w <¥). Не трудно доказать, что при отрицательных значениях частот годограф симметричен годографу при положительных значениях частот (относительно вещественной оси).
Рисунок 1 - Годограф Найквиста 2 Диаграммы Боде Логарифмические амплитудные и фазовые частотные характеристики (ЛЧХ), называемые диаграммами Боде, получили гораздо большее распространение, чем годографы Найквиста. Прологарифмировав выражение частотной характеристики (через амплитудную и фазовую), получим, что ее логарифм равен сумме логарифма амплитудной характеристики и фазовой характеристики:
Две характеристики В теории автоматического управления используются десятичные логарифмы. За единицу измерения принимается децибел ( Логарифмический масштаб частот связан с некоторыми особенностями в терминологии. При двукратном изменении частот говорят, что частота изменилась на октаву, а при десятикратном – на декаду. Иначе говоря, октава – отрезок логарифмической оси частот, между произвольным значением частоты и ее удвоенным значением. Декада – отрезок логарифмической оси частот между произвольным значением частоты и в десять раз большим значением:
При графическом изображении логарифмических характеристик придерживаются некоторых правил. Точка, соответствующая нулевому значению частоты лежит слева в бесконечности, т.к. lg0 = -¥. Поэтому ось ординат проводится через любую точку оси частот так, чтобы справа располагалась та часть ЛЧХ, которую нужно исследовать, а слева – для описания которой достаточно качественных характеристик. Слева обычно остается та часть фазовой характеристики, которая мало отличается от нуля (или другого постоянного значения). То же самое можно сказать и о коэффициенте наклона амплитудной характеристики. Слева обычно оставляют ту часть амплитудной характеристики, коэффициент наклона которой мало отличается от нулевого значения (или другого постоянного значения. Амплитудную и фазовую характеристики изображают на одном рисунке с общей осью частот. Ось частот разбивается на декады и, может быть, октавы, причем каждая декада разбивается на октавы отдельно. Для удобства под точками этой оси принято записывать не значения логарифмов частот, а значения самих частот. Обе характеристики имеют общую ось ординат, но две разные разметки: в децибелах для амплитудной характеристики и в радианах (или градусах) для фазовой. Удобство логарифмических характеристик заключается в возможности простого определения амплитудных характеристик последовательного соединения звеньев и спрямления амплитудных характеристик, как будет показано ниже. Передаточная функция последовательного соединения звеньев равна произведению передаточных функций соединяемых звеньев. Поэтому
Вместе с тем
Определим отсюда выражение логарифмических характеристик последовательного соединения звеньев:
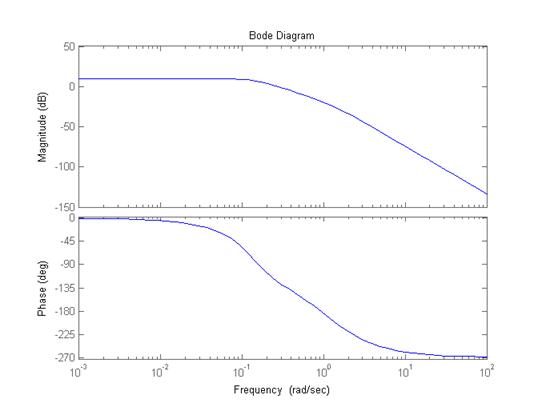
Таким образом, логарифмические характеристики последовательного соединения складываются. Это относится как к амплитудным, так и к фазовым характеристикам. На рисунке 2 в качестве примера изображены логарифмические характеристики (диаграммы Боде) системы с передаточной функцией
Рисунок 2 - Логарифмические частотные характеристики (ЛЧХ) |
||||
Чтобы скачать материал, пожалуйста, авторизуйтесь или зарегистрируйтесь! Это быстро ! )
Категории
| Математика, алгебра, геометрия [1729] |
| Книги (Это интересно) [351] |
| Видеоуроки [26920] |
| География [2660] |
| Дополнительное образование [401] |
| ЕГЭ/ГИА [266] |
| Информатика [1187] |
| История / обществознание [4663] |
| Для Логопеда [500] |
| Материалы для коррекц. классов [400] |
| ОБЖ [558] |
| Презентации [402] |
| Для Психолога [514] |
| Физическая культура [529] |
| Черчение [121] |
| Шаблоны презентаций [466] |
| Для Библиотекаря [160] |
| Праздники [419] |
| Интересные Видеоролики [12] |
| Английский язык [791] |
| Иностранные языки (прочие) [461] |
| Окружающий мир [873] |
| Биология и экология [1643] |
| Всем учителям [508] |
| Для директора и завуча [1042] |
| Дошкольное образование [1238] |
| Искусство [804] |
| Для Классного руководителя [543] |
| Начальные классы [718] |
| Основы религиозных культур [137] |
| Программы и Софт [21] |
| Родной язык [505] |
| Русский язык и литература [3915] |
| Технология [1000] |
| Физика [1263] |
| Химия [1297] |
| Экономика [905] |
| Астрономия [444] |
| Писатели [113] |
| Классный час [527] |
| Шаблоны документов [85] |
| Другое (Прочее) [412] |





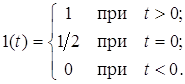
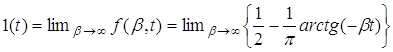 .
.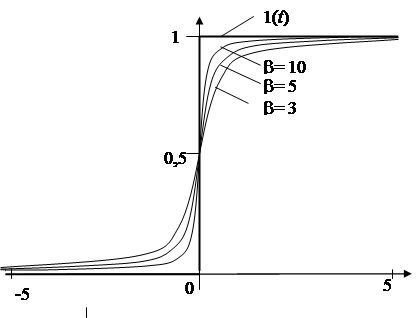
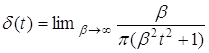 .
.
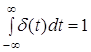 .
.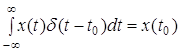 ,
,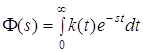 ,
,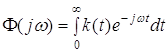 ,
, 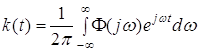 .
.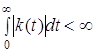 .
.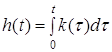 .
.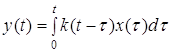 (1)
(1)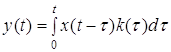 . (2)
. (2)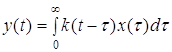
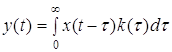 .
.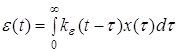 .
.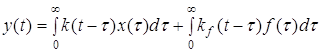 ,
,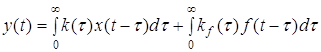 .
.